_edited.jpg)
What is the van Hiele Model
of Geometric Thinking?

While there is no specific grade level attachment to the van Hiele model of Geometric Thinking, when thinking about the Common Core State Standards, achieving Level 2: Informal Deduction, is an excellent goal for the end of 5th grade.
Level 0:Visualization
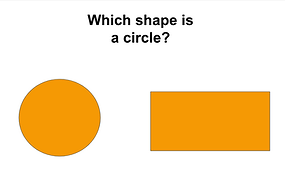
The most basic level of understanding geometric concepts is visualization. this level focuses on recognizing a "whole" shape and connecting that shape to a real-world object. For example, children might say that a square or rectangle looks like a window. Children at this level are not identifying any properties of shapes, but might be able to say "it is a circle/ it is not a circle," for instance.
Level 1: Analysis

At Level 1, children start attaching properties to shapes, such as a triangle has three sides, or a square has four sides that are all the same length. Children at this level are able to fold and cut paper.
Level 2: Informal Deduction


Children at this level are able to find relationships between shapes and their properties. Completing a Venn Diagram, to determine similarities and differences of shapes and their properties, is a good activity to determine if children are at this level.
Level 3: Deduction
Individuals at this level are able to generalize and use the properties of shapes to prove that a shape is indeed that shape. At this level, individuals are able to write proofs and understand the role of definitions.
Level 4: Rigor
This final level is reserved for individuals who have a generalized understanding of geometric principles and different types of proofs. Individuals at this level might be majoring in mathematics at a collegiate level.
Continue to Explore Kids Math Talk - Geometry for suggestions of Geometry talks, as well as links to professional learning resources.
Visit the Geometry Talk- Articles to Explore for links to more examples of the van Hiele Model of Geometric Thinking.